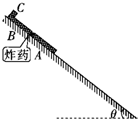
如图所示,在倾角θ=37°的足够长的光滑斜面上,质量都为M=2kg的长方体板A和B之间夹有少许炸药,在B的上表面左端叠放有一质量m=1kg的物体C(可视为质点),C与B之间的动摩擦因数μ=0.75.现无初速度同时释放A、B、C整体,当它们沿斜面滑行s=3m时,炸药瞬间爆炸,爆炸完毕时A的速度vA=12m/s.此后,C始终未从B的上表面滑落.问:B的长度至少为多大?(取g=10m/s2,爆炸不会影响各物体的质量和各表面的光滑程度)
整体下滑阶段,研究A、B、C整体,设末速度为v,由动能定理得:
(2M+m)gssinθ=
(2M+m)v2 1 2
解得:v=
=2gssinθ
m/s=6m/s2×10×3×0.6
爆炸前后,A和B组成的系统动量守恒,由动量守恒定律有:
2Mv=MvA+MvB
解得:vB=0
此后,设C在B上滑动的加速度为aC,由牛顿第二定律有:
mgsinθ-μmgcosθ=maC
解得:aC=g(sinθ-μcosθ)=10×(0.6-0.75×0.8)=0
对B,由牛顿第二定律有:Mgsinθ+μmgcosθ=MaB
得:
aB=gsinθ+
cosθ=10×0.6+μmg M
×0.8=9(m/s2)0.75×1×10 2
C和B经时间t达到共同速度v后将不再相对滑动,则有:t=v aB
板的最小长度L满足:L=vt-
t v 2
联立解得:L=2m.
答:B的长度至少为2m.
