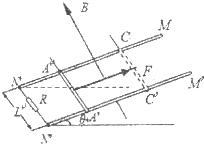
如图所示,宽为L=0.5m、足够长的平行金属导轨MN和M’N’固定在倾角为θ=37°的斜面上,在N和N’之间连有一个0.8Ω的电阻R.在导轨上AA’处放置一根与导轨垂直、质量为m=0.2kg、电阻r=0.2Ω的金属棒,导轨电阻均不计.在导轨所围的区域存在一个磁感应强度B=2.0T、方向垂直于斜面向上的匀强磁场,已知金属棒和导轨间的动摩擦因数为μ=0.25.现在金属棒中点施加一个垂直于金属棒且沿斜面向上的外力F,使金属棒从静止开始以加速度a=lm/s2沿斜面向上做匀加速直线运动,经3s恰好经过CC‘处.求:
(1)金属棒从AA‘运动到CC‘过程中通过R的电荷量;
(2)金属棒通过CC‘时所施加的外力F的大小;
(3)如果在此过程中外力F所做的功为17.1J,求在此过程中金属棒放出的焦耳热是多少?
(1)金属棒从AA′开始做匀加速运动的过程中,其位移为:
x=
at2=1 2
×1××32m=4.5m1 2
由:
=. E
、△Φ △t
=. I
、q=. E R+r
•△t. I
得电量:q=
=BLx R+r
C=4.5C.2×0.5×4.5 0.8+0.2
(2)金属棒运动到CC′时:
v=at=3m/s
感应电动势:E=BLv,I=
=E R+r BLat R+r
根据牛顿第二定律得:
F-mgsinθ-μmgcosθ-BIL=ma
解得,F=4.8N
(3)在此过程中,对金属棒运用动能定理得:
W-mgsinθ•x-μmgcosθ•x-W安=
mv21 2
解得:Q=W安=9J
根据焦耳定律得知,金属棒放出的焦耳热为:
Qr=
Q=1.8Jr r+R
答:(1)从AA‘运动到CC‘过程中通过R的电荷量是4.5C;
(2)金属棒通过CC′时所施加的外力F的大小是4.8N;
(3)金属棒放出的焦耳热为1.8J.
