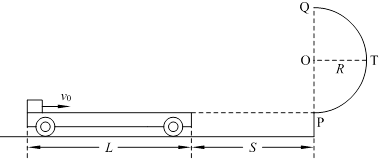
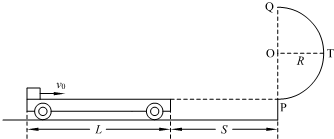
如图所示,地面和半圆轨道面均光滑.质量M=1kg、长L=4m的小车放在地面上,其右端与墙壁的距离为S=3m,小车上表面与半圆轨道最低点P的切线相平.现有一质量m=2kg的滑块(不计大小)以v0=6m/s的初速度滑上小车左端,带动小车向右运动.小车与墙壁碰撞时即被粘在墙壁上,已知滑块与小车表面的滑动摩擦因数μ=0.2,g取10m/s2.
(1)求小车与墙壁碰撞时的速度;
(2)要滑块能沿圆轨道运动而不脱离圆轨道,求半圆轨道的半径R的取值.
(1)设滑块与小车的共同速度为v1,滑块与小车相对运动过程中动量守恒,有
mv0=(m+M)v1
代入数据解得
v1=4m/s
设滑块与小车的相对位移为 L1,由系统能量守恒定律,有
μmgL1=
m1 2
-v 20
(m+M)1 2 v 21
代入数据解得 L1=3m
设与滑块相对静止时小车的位移为S1,根据动能定理,有
μmgS1=
M1 2
-0v 21
代入数据解得S1=2m
因L1<L,S1<S,说明小车与墙壁碰撞前滑块与小车已具有共同速度,且共速时小车与墙壁还未发生碰撞,故小车与碰壁碰撞时的速度即v1=4m/s.
(2)滑块将在小车上继续向右做初速度为v1=4m/s,位移为L2=L-L1=1m的匀减速运动,然后滑上圆轨道的最低点P.
若滑块恰能滑过圆的最高点,设滑至最高点的速度为v,临界条件为
mg=mv 2 R
根据动能定理,有
-μmgL2-mg•2R=
mv 2-1 2
m1 2 v 21
①②联立并代入数据解得R=0.24m
若滑块恰好滑至
圆弧到达T点时就停止,则滑块也能沿圆轨道运动而不脱离圆轨道.1 4
根据动能定理,有
-μmgL2-mg•R=0-
m1 2 v 21
代入数据解得R=0.6m
综上所述,滑块能沿圆轨道运动而不脱离圆轨道,半圆轨道的半径必须满足
R≤0.24m或R≥0.6m
答:
(1)小车与墙壁碰撞时的速度是4m/s;
(2)要滑块能沿圆轨道运动而不脱离圆轨道,半圆轨道的半径R的取值为R≤0.24m或R≥0.6m.
