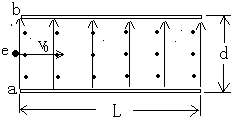
如图所示:两块带电金属板a、b水平正对放置,在板间形成匀强电场,电场方向竖直向上.板间同时存在与电场正交的匀强磁场,假设电场、磁场只存在于两板间的空间区域.一束电子以一定的初速度v0从两板的左端中央,沿垂直于电场、磁场的方向射入场中,无偏转的通过场区.
已知:板长L=10.0cm,两板间距d=3.0cm,两板间电势差U=150V,v0=2.0×107m/s.电子所带电量与其质量之比e/m=1.76×1011C/kg,电子电荷量1.60×10-19C,不计电子所受的重力和电子之间的相互作用力.求:
(1)求磁感应强度B的大小
(2)若撤去磁场,求电子离开电场时偏离入射方向的距离y
(3)若撤去磁场,求电子穿过电场的整个过程中动能的增加量△EK(4).
(1)由平衡条件得
e
=ev0B,得,B=U d
=2.5×10-4TU v0d
(2)若撤去磁场,电子做平抛运动.
水平方向:L=v0t
竖直方向:y=
at2,a=1 2 eU md
联立得到,y=eUL2 2md v 20
代入解得,y=1.1×10-2m
(3)根据动能定理得
动能的增加量△EK=eEy=e
yU d
代入解得,△EK=8.8×10-18J
答:
(1)磁感应强度B的大小为2.5×10-4T.
(2)若撤去磁场,求电子离开电场时偏离入射方向的距离y=1.1×10-2m.
(3)若撤去磁场,求电子穿过电场的整个过程中动能的增加量△EK=8.8×10-18J.
