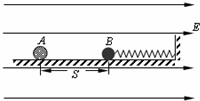
如图所示,劲度系数为k的轻弹簧,左端连着绝缘介质小球B,右端连在固定板上,放在光滑绝缘的水平面上.整个装置处在场强大小为E、方向水平向右的匀强电场中.现有一质量为m、带电荷量为+q的小球A,从距B球为S处自由释放,并与B球发生碰撞.碰撞中无机械能损失,且A球的电荷量始终不变.已知B球质量为A球质量的3倍,A、B小球均可视为质点.求:
(1)A球与B球碰撞前瞬间的速度v0;
(2)求A球与B球第一次碰撞后瞬间,A球的速度v1和B球的速度v2;
(3)B球被碰后的运动为周期性运动,其运动周期T=2π,要使A球与B球第二次仍在B球的初始位置迎面相碰,求劲度系数k的可能取值.
(1)设A球与B球碰撞前瞬间的速度为v0,
由动能定理得,qES=m
解得:v0=
(2)碰撞过程中动量守恒,则有 mv0=mv1+Mv2
机械能无损失,有 m=m+M
联立上两式解得 v1=-v0=- 方向向左,v2=v0= 方向向右.
(3)要使m与M第二次迎面碰撞仍发生在原位置,则必有A球重新回到O处所用的时间t恰好等于B球的(n+)T.(n=0、1、2、3 …)
A球运动的加速度为 a=,t==(n+)T,
又由题意,T=2π,解得:k=(n+)2(n=0、1、2、3 …)
答:
(1)A球与B球碰撞前瞬间的速度v0是.
(2)A球与B球第一次碰撞后瞬间,A球的速度v1大小,方向向左.B球的速度v2是,方向向右.
(3)劲度系数k的可能取值是k=(n+)2(n=0、1、2、3 …).