问题
解答题
已知圆C经过P（4，-2），Q（-1，3）两点，且在y轴上截得的线段长为4，半径小于5．
（1）求直线PQ与圆C的方程；
（2）若直线l∥PQ，且l与圆C交于点A、B，∠AOB=90°，求直线l的方程．
答案
解：（1）直线PQ的方程为y-3=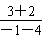
×（x+1），即x+y-2=0，
C在PQ的中垂线y-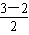
=1×（x-
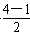），即y=x-1上，
设C（n，n-1），
则r2=|CQ|2=（n+1）2+（n-4）2，
由题意，有r2=（2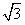
）2+|n|2，
∴n2+12=2n2-6n+17，
∴n=1或5，r2=13或37（舍去），
∴圆C为（x-1）2+y2=13．
（2）设直线l的方程为x+y+m=0，
由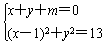
，得2x2+（2m-2）x+m2-12=0，
设A（x1，y1），B（x2，y2），则x1+x2=1-m，x1x2=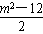
，
∵∠AOB=90°，
∴x1x2+y1y2=0，
∴x1x2+（x1+m）（x2+m）=0，
∴m2+m-12=0，∴m=3或-4（均满足Δ＞0），
∴l为x+y+3=0或x+y-4=0．