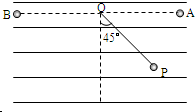
如图所示,一质量为m带正电的小球,用长为L的绝缘细线悬挂于O点,处于一水平方向的匀强电场中,静止时细线右偏与竖直方向成45°角,位于图中的P点.重力加速度为g,求:
(1)静止在P点时线的拉力是多大?
(2)如将小球向右拉紧至与O点等高的A点由静止释放,则当小球摆至P点时,其电势能如何变?变化了多少?
(3)如将小球向左拉紧至与O点等高的B点由静止释放,则小球到达P点时的速度大小?
(1)小球静止在P点时由平衡条件得
cos45°=mg T
T=
mg2
(2)小球从A到P的过程中,电场力做负功,故其电势能增加
由(1)问得tan45°=
F电=mgF电 mg
则小球克服电场力做功W=F电L(1-cos45°)
其电势能增加为△EP=△W=
mgL2- 2 2
(3)小球先做匀加速直线运动到达最低点C,
根据动能定理得:
mvC2-0=mgL+F电L vC=21 2 gL
到达C点后细绳绷紧,小球沿细绳方向的速度变为零,
则vC′=vCsin45° vC′=2gL
从C到P做圆周运动,由动能定理得:
mvP2-1 2
mvC^2=-mgL(1-cos45°)+F电Lsin45°1 2
vP=2
gL2
答:(1)静止在P点时线的拉力是
mg.2
(2)如将小球向右拉紧至与O点等高的A点由静止释放,当小球摆至P点时,其电势能增加了
mgL.2- 2 2
(3)如将小球向左拉紧至与O点等高的B点由静止释放,小球到达P点时的速度 vP=
.2
gL2
