问题
问答题
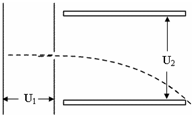
如图所示,有一质子(电量为e,质量为m)由静止经电压U1加速后,进入两块间距为d电压为U2的平行金属板间,若质子从两板正中间垂直电场方向射入,且正好能从下板右边缘穿出电场,求:
(1)质子则进入偏转电场U2时的速度;
(2)在偏转电场U2中运动的时间和金属板的长L;
(3)质子穿出电场时的动能.
答案
(1)质子在左边的加速电场中有:qU1=
m1 2 v 20
解得
v0=2qU1 m
即质子则进入偏转电场U2时的速度为
.2qU1 m
(2)质子在右边的偏转电场中可分解为沿板方向的匀速直线运动和垂直板方向的匀加速直线运动
所以沿板方向:x=L=v0t ①
垂直板方向:y=
d=1 2
at2 ②1 2
而加速度:a=
=F m
③qU md
由以上各式解得
极板长为L=
d2U0 U
时间t为md2 qU
即在偏转电场U2中运动的时间为
、金属板的长Lmd2 qU
d.2U0 U
(3)质子先在加速电场中电场力对其做正功,而后又在偏转电场中,尽管做曲线运动,但电场力对它仍然做正功,且电场力做功与路径无关.所以整个过程由动能定律得:eU0+e
=Ek-0U 2
所以质子射出电场时的动能为:Ek=e(U0+
)U 2
即质子穿出电场时的动能为e(U0+
).U 2
