问题
问答题
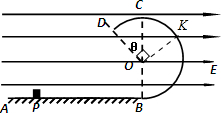
如图所示,水平绝缘光滑轨道AB与处于竖直平面内的圆弧形v绝缘光滑轨道BCD平滑连接,圆弧形轨道的半径R=0.30m.轨道所在空间存在水平向右的匀强电场,电场强度E=1.0×107 N/C.现有一电荷量q=-4.0×10-7C,质量m=0.30kg的带电体(可视为质点),在水平轨道上的P点以某一水平初速度v0向右运动,若带电体恰好可以沿圆弧轨道运动到D点,并在离开D点后,落回到水平面上的P点.,已知OD与OC的夹角θ=37°,求:
(1)P、B两点间的距离x;
(2)带电体经过C点时对轨道的压力;
(3)小球的初速度v0的值.

答案
(1)等效重力mg′=
=5N,方向:垂直OD斜向下(Eq)2+(mg)2
故根据几何关系,有
x=
+R sin37°
=0.9mR tan37°
即PB间距为0.9.
(2)令电荷经过等效最高点K的速度为v,如图
则在K点重力恰好提供向心力
=mg′ ①mv2 R
从k到c过程,根据动能定理,有
mvc2-1 2
mv2=mg′R(1-sin37°)1 2
在C点重力和弹力的合力提供向心力,有
=FN+mgmvc2 R
解得:FN=6N
故带电体经过C点时对轨道的压力为6N.
(3)对从A大K过程运用动能定理,得到
mv2-1 2
mv02=-mg′(x+R) ②1 2
由①②,解得
v0=3
m/s5
故小球的初速度v0的值为3
m/s.5
