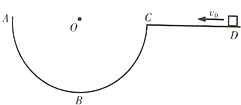
如图所示,半径r=0.80m的光滑金属半球壳ABC与水平面在C点连接,一质量m=0.10kg的小物块在水平面上距C点s=1.25m的D点,以不同的初速度向C运动.O点是球心,D、C、O三点在同一直线上,物块与水平面间的动摩擦因数µ=0.20,取g=10m/s2.
(1)若物块运动到C点时速度为零,恰好沿球壳滑下,求物块滑到最低点B时对球壳的压力大小.
(2)若物块运动到C点水平飞出,恰好落在球壳的最低点B,求物块在D点时的初速度大小.
(3)通过分析判断小物块能否垂直撞击球壳.
(1)设小物块滑到最低点B的速度为vB,受到球壳的支持力为NB,则在小物块从C至B的过程中只有重力做功,根据动能定理有:
mgr=
m1 2
-0v 2B
可得:vB=2gr
小物块在B点所受合力提供其圆周运动向心力,根据牛顿第二定律有:
NB-mg=mv 2B r
得:NB=mg+m
=mg+mv 2B r
=3mg=33×10×0.1N=3N2gr r
根据牛顿第三定律可知,小物块在B点对半球壳的压力为3N;
(2)小物块从C点水平滑出做平抛运动,其恰好落在B点,则可知小物块在平抛过程中:
水平位移x=r=vct…①
竖直位移y=r=
gt2…②1 2
由①和②可得:vC=
=r t
=r 2r g
=gr 2
m/s=2m/s10×0.8 2
小物块在从D到C的过程中只有滑动摩擦力做功,根据动能定理有:
-μmgs=
m1 2
-v 2C
m1 2 v 2D
解得:vD=
=
+2μgsv 2C
m/s=3m/s22+2×0.2×1.25
(3)若物块撞击球壳BC段,速度方向斜向左下方,则不可能垂直撞击半球壳,若小球落在AB上的E点,OE与竖直方向的夹角为θ,E点时速度与竖直方向夹角为α,则小球从C到E做平抛运动有:
竖直方向位移:y=rcosθ=
gt2,1 2
所以其运动时间为:t=2rcosθ g
在E点竖直分速度:vy=gt=2grcosθ
小物块在水平方向的位移为:x=r+rsinθ=vCt=vC2rcosθ g
在E点水平分速度:vc=r+rsinθ 2rcosθ g
所以在E点小物块速度方向与竖直方向的夹角的正切值:
tanα=
=vx vy
=r+rsinθ 2rcosθ g 2grcosθ
=r+rsinθ 2rcosθ 1+sinθ 2cosθ
因为:tanα=
>tanθ1+sinθ 2cosθ
所以小球不可能垂直撞击球壳.
答:(1)若物块运动到C点时速度为零,恰好沿球壳滑下,物块滑到最低点B时对球壳的压力大小为3N;
(2)若物块运动到C点水平飞出,恰好落在球壳的最低点B,物块在D点时的初速度大小为3m/s;
(3)小球不可能垂直撞击球壳.
