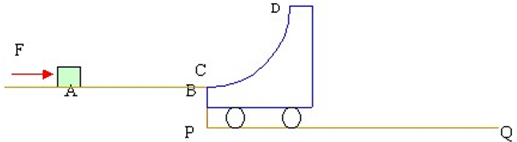
如图所示,质量为m=0.4kg的滑块,在水平外力F作用下,在光滑水平面上从A点由静止开始向B点运动,到达B点时外力F突然撤去,滑块随即冲上半径为R=0.4米的
光滑圆弧面小车,小车立即沿光滑水平面PQ运动.设:开始时平面AB与圆弧CD相切,A、B、C三点在同一水平线上,令AB连线为X轴,且AB=d=0.64m,滑块在AB面上运动时,其动量随位移的变化关系为P=1.61 4
kgm/s,小车质量M=3.6kg,不计能量损失.X
求:
(1)滑块受水平推力F为多大?
(2)滑块到达D点时,小车速度为多大?
(3)滑块返回C点时小车与滑块的速度分别为多大?
(4)滑块从D点滑出再返回D点这一过程中,小车移动距离为多少?(g取10m/s2)
(1)由P=1.6
=mv,代入x=0.64m,可得滑块到B点速度为:X
VB=
=1.6 X m
m/s=3.2 m/s1.6 0.64 0.4
A→B,由动能定理得:FS=
mVB21 2
所以 F=m
=vB2 2S
N=3.2N 0.4×3.22 2×0.64
(2)滑块由C→D的过程中,滑块和小车组成系统在水平方向动量守恒,由于滑块始终紧贴着小车一起运动,在D点时,滑块和小车具有相同的水平速度VDX.
由动量守恒定律得:mVC=(M+m)VDXVC=VB
所以 VDX=
=0.32m/s mVC M+m
(3)以滑块、小车为系统,以滑块滑上C点为初态,滑块第二次滑到C点时为末态,此过程中系统水平方向动量守恒,系统机械能守恒得:
mVC=mVC′+MV
mVC2=1 2
mVC′2+1 2
MV21 2
上式中VC′、V分别为滑块返回C点时,滑块与小车的速度,
V=0.64m/s
VC′=-2.56m/s (负号表示与V反向 )
(4)由机械能守恒定律,滑快由C到D,对系统有:
mVC2=mgR+1 2
M VDX2+1 2
m(VDX2+VDY2)1 2
所以 VDY=1.1m/s
滑块离D到返回D这一过程中,小车做匀速直线运动,前进距离为:
S=
=VDX2VDY g
m=0.07m 0.32×2×1.1 10
答:(1)滑块受水平推力F为3.2N;
(2)滑块到达D点时,小车速度为0.32m/s
(3)滑块返回C点时小车的速度为-2.56m/s,滑块的速度为0.64m/s;
(4)滑块从D点滑出再返回D点这一过程中,小车移动距离为0.07m.
