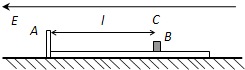
如图所示,光滑水平面上放有用绝缘材料制成的“L”型滑板,其质量为M,平面部分的上表面光滑且足够长.在距滑板的A端为l的B处放置一个质量为m、带电量为q的小物体C(可看成是质点),在水平的匀强电场作用下,由静止开始运动.已知:M=3m,电场的场强为E.假设物体C在运动中及与滑板A端相碰时不损失电量.
(1)求物体C第一次与滑板A端相碰前瞬间的速度大小.
(2)若物体C与滑板A端相碰的时间极短,而且碰后弹回的速度大小是碰前速度大小的
,求滑板被碰后的速度大小.1 5
(3)求小物体C从开始运动到与滑板A第二次碰撞这段时间内,电场力对小物体C做的功.
(1)设物体C在电场力作用下第一次与滑板的A段碰撞时的速度为v1,由动能定理得:
qEl=
mv12 解得:v1=1 2 2qEl m
(2)小物体C与滑板碰撞过程中动量守恒,设滑板碰撞后的速度为v2,由动量守恒定律得
mv1=Mv2-m
v11 5
解得:v2=
v1=2 5 2 5 2qEl m
(3)小物体C与滑板碰撞后,滑板向左作以速度v2做匀速运动;小物体C以
v1的速度先向右做匀减速运动,然后向左做匀加速运动,直至与滑板第二次相碰,设第一次碰后到第二次碰前的时间为t,小物体C在两次碰撞之间的位移为s,根据题意可知,小物体加速度为1 5
a=qE m
小物体C与滑板从第一次碰后到第二次碰时位移相等,即
v2t=-
v1t+1 5
at2 解得:t=1 2 6 5 2ml qE
两次相碰之间滑板走的距离s=v2t=
l24 25
设小物体C从开始运动到与滑板A第二次碰撞这段过程电场力对小物体做功为W,则:W=qE(l+s)
解得:W=
qEl49 25
答:(1)物体C第一次与滑板A端相碰前瞬间的速度大小是
.2qEl m
(2)滑板被碰后的速度大小是2 5
.2qEl m
(3)电场力对小物体C做的功W=
qEl.49 25
