问题
问答题
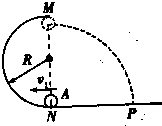
半径R=20cm的竖直放置的圆轨道与平直轨道相连接,如图所示.质量m=50g的小球A以一定的初速度由直轨道向左运动,并沿圆轨道的内壁冲上去.如果球A经过N点时速度v1=4m/s,球A经过轨道最高点M时对轨道的压力为0.5N,取g=10m/s2,求:
(1)小球落地点P与N之间的距离?
(2)小球从N运动到M这一段过程中克服阻力做的功?
答案
(1)根据牛顿第二定律,设小球在M点的速度为v2,有
N+mg=mv2 R
根据平抛运动规律有:2R=
gt2 s=vt 1 2
联立方程代数解得:s=0.56m
小球落地点P与N之间的距离为0.56m.
(2)小球从M到N过程,据动能定理
mg(2R)-w=
mv22-1 2
mv121 2
解得w=mg(2R)-
mv22+1 2
mv121 2
代数解得 W=0.1J
小球从N运动到M这一段过程中克服阻力做的功为0.1J.
