问题
解答题
已知点P(2,0)及圆C:x2+y2-6x+4y+4=0。
(1)若直线l过点P且与圆心C的距离为1,求直线l的方程;
(2)设过点P的直线l1与圆C交于M、N两点,当|MN|=4时,求以线段MN为直径的圆Q的方程;
(3)设直线ax-y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l2垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由。
答案
解:(1)设直线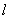 的斜率为k(k存在),
的斜率为k(k存在),
则方程为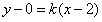 ,即
,即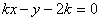 ,
,
又圆C的圆心为(3,-2),半径r=3,
由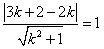 , 解得
, 解得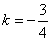 ,
,
所以,直线的方程为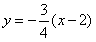 ,即
,即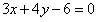 ,
,
当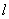 的斜率不存在时,
的斜率不存在时,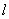 的方程为x=2,经验证x=2也满足条件。
的方程为x=2,经验证x=2也满足条件。
(2)由于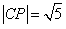 ,而弦心距
,而弦心距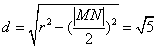 ,
,
所以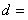
 ,
,
所以P恰为MN的中点,
故以MN为直径的圆Q的方程为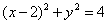 。
。
(3)把直线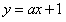 ,代入圆C的方程,
,代入圆C的方程,
消去y,整理得 ,
,
由于直线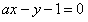 交圆C于A,B两点,
交圆C于A,B两点,
故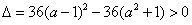 ,
,
即 ,解得:
,解得: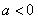 ,
,
则实数a的取值范围是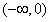 。
。
设符合条件的实数a存在,由于 垂直平分弦AB,故圆心C(3,-2)必在
垂直平分弦AB,故圆心C(3,-2)必在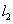 上,
上,
所以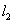 的斜率
的斜率 ,而
,而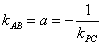 ,所以
,所以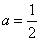 ,
,
由于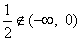 ,
,
故不存在实数a,使得过点P(2,0)的直线 垂直平分弦AB。
垂直平分弦AB。
