问题
多选题
如图所示，在竖直平面内有一半径为R的圆弧轨道，半径OA水平、OB竖直，一个质量为m的小球自A的正上方P点由静止开始自由下落，小球沿轨道到达最高点B时恰好对轨道没有压力．已知AP=2R，重力加速度为g，则小球从P到B的运动过程中（ ）
A．重力做功mgR
B．机械能减少mgR
C．合外力做功mgR
D．克服摩擦力做功1 2mgR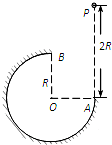 
答案
A、重力做的功WG=mgh=mgR，故A正确；
B、小球在B时恰好对轨道没有压力，重力提供向心力，由牛顿第二定律得：mg=m
，vB=v 2B R
，从P到B的过程，由动能定理可得：mgR-Wf=gR
mvB2-0，Wf=1 2
mgR，则物体机械能较少1 2
mgR，故B错误；1 2
C、由动能定理可得，合外力做的功W=
mvB2=1 2
mgR，故C错误；1 2
D、由B可知，克服摩擦力做功
mgR，故D正确；1 2
故选AD．
