问题
问答题
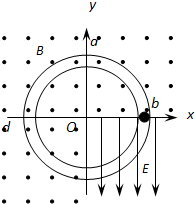
如图所示,一光滑绝缘圆管轨道位于竖直平面内,半径为0.2m.以圆管圆心O为原点,在环面内建立平面直角坐标系xOy,在第四象限加一竖直向下的匀强电场,其他象限加垂直于环面向外的匀强磁场.一带电量为+1.0C、质量为0.1kg的小球(直径略小于圆管直径),从x坐标轴上的b点由静止释放,小球刚好能顺时针沿圆管轨道做圆周运动.(重力加速度g取10m/s2)
(1)求匀强电场的电场强度E;
(2)若第二次到达最高点a时,小球对轨道恰好无压力,求磁感应强度B;
(3)求小球第三次到达最高点a时对圆管的压力.
答案
(1)小球第一次刚好过最高点,此时速度v1=0
根据动能定理得,qER-mgR=0
∴E=
=1N/Cmg q
(2)小球第二次过最高点是速度为v2,由动能定理可知2qER-mgR=
m1 2 v 22
又mg+qv2B=m
.v 22 R
以上两式可解得B=m q
=0.5Tg 2R
(3)小球第三次过最高点时速度为,小球受圆管向下的压力为FN
3qER-mgR=
m1 2 v 23
mg+qv3B+FN=mv 23 R
解得FN=(3-
)mg=(3-2
)N2
根据牛顿第三定律可知
小球第三次到达最高点a时对圆管的压力为(3-
)N方向竖直向上.2
答:(1)匀强电场的电场强度为1N/C.(2)磁感应强度B为0.5T.(3)小球第三次到达最高点a时对圆管的压力为(3-
)N,方向竖直向上.2
