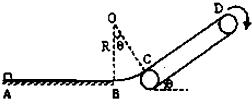
如图所示,光滑圆弧面BC与水平面和传送带分别相切于B、C两处,OC垂直于CD.圆弧所对的圆心角θ=37°,BC圆弧半径R=7m.足够长的传送带以恒定速率v=4m/s顺时针转动,传送带CD与水平面的夹角θ=37°.一质量m=1kg的小滑块从A点以v0=1Om/s的初速度向B点运动,A、B间的距离s=3.6m.小滑块与水平面、传送带之间的动摩擦因数均为u=0.5.重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8.求:
(1)小滑块第一次滑到C点时的速度;
(2)小滑块到达的最高点离C点的距离;
(3)小滑块最终停止运动时距离B点的距离;
(4)小滑块返回圆弧最低点B时对轨道的压力.
(1)C离A的高度:h=R-Rcosθ=R-0.8R=0.2R=1.4m
滑块从A到C的过程中有:-mgh-μmgs=
m1 2
-v 2c
m1 2 v 20
代入数据解得:vc=6m/s.
(2)物体在传送带上运动的加速度大小为a1,则:
a1=gsinθ+μgcosθ=10×sin37°+0.5×10×cos37°=10m/s 2,
设物体在传送带上达到与传送带等速时的时间为t 1,则:v=vc-a1t1
得:t1=
=vc-v a1
s=0.2s.6-4 10
向上的位移:x1=vct1-
a11 2
=6×0.2-t 21
×10×0.22=1m1 2
由于:mgsinθ>μmgcosθ
物体继续在传送带上减速上滑,加速度:
a2=gsinθ-μgcosθ=10×sin37°-0.5×10×cos37°=2m/s2
继续向上滑动的时间:t2=
=v a2
s=2s4 2
继续向上滑动的位移:x2=vt2-
a21 2
=4×2-t 12
×2×22=4m1 2
向上运动的最大距离:x=x1+x2=1m+4m=5m.
(3)滑块沿传送带返回C点的过程中:
=2a2xv 2C2
得:vC2=
=2a2x
=22×2×5m/s
m/s5
根据动能定理得,物体从C到停止:0-
m1 2
=mgh-μmgsv 2C2
代入数据解得:s=4.8m
(4)设滑块在B点的速度是vB,则:0-
m1 2
=-μmgsv 2B
又:FN-mg=m v 2B R
得:FN=mg+
=mg+m v 2B R
=1×10+2μmgs R
≈17N2×0.5×10×4.8 7
答:(1)小滑块第一次滑到C点时的速度是6m/s;
(2)小滑块到达的最高点离C点的距离是5m;
(3)小滑块最终停止运动时距离B点的距离是4.8m;
(4)小滑块返回圆弧最低点B时对轨道的压力是17N.
