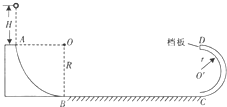
如图所示，AB和CD处于竖直平面内的光滑圆弧轨道，OA处于水平位置

问题问答题

如图所示，AB和CD处于竖直平面内的光滑圆弧轨道，OA处于水平位置．AB是半径为R=2m的

的圆周轨道，CD是半径为r=1m的半圆圆管轨道（圆管宽度可以忽略），最高点D处于固定一个竖直弹性挡板，小球与挡板碰撞后功能损失不计．BC是水平粗糙轨道，与圆弧形轨道平滑连接．已知BC段水平轨道L=4m，与小球之间的动摩擦因数μ=0.1．现让一个质量m=1kg的小球p从A点的正上方距水平线OA高H=1.9m处自由落下，g取10m/s²．求：

（1）小球第一次到达D点对轨道的压力和方向；

（2）小球与弹性挡板碰撞额次数，小球最终静止于何处．

答案

（1）根据动能定理得，mgH+mgR-μmgL-mg2r=

mvD2

vD=

2gH-2μgL

2×10×1.9-2×0.1×10×4

m/s，

由圆周运动得，mg+FN=m

代入数据解得F_N=20N，

由牛顿第三定律得，轨道所受压力大小为20N，方向竖直向上．

（2）小球要想碰撞D处挡板的临界速度v＞0，由临界情况时的功能关系可得：

mgH+mgR-μmgX_L′-mg2r＞0

所以XL′＜

=19m．

由小球碰撞运动的情境可得，第一次碰撞运动L，第二次碰撞运动了3L，第三次碰撞运动了5L，

所以小球与挡板碰撞了2次．

小球最终将停于BC上，满足mgH+mgR-μmgX_L=0，

X_L是L长度的9.75倍．

最终小球由B点返回时停于距B点1m处（或距C点3m处）．

答：（1）小球第一次到达D点对轨道的压力大小为20N，方向竖直向上．

（2）小球与弹性挡板碰撞的次数为2次．最终小球由B点返回时停于距B点1m处．