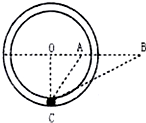
如图所示,在竖直面上固定着一根光滑绝缘的圆形空心管,其圆心在O点.过O点的一条水平直径上的A、B两点固定着两个点电荷.其中固定于A点的为正电荷,电荷量大小为Q;固定于B点的是未知电荷.在它们形成的电场中,有一个可视为质点的质量为m、电荷量大小为q的带电小球正在空心管中作圆周运动,若已知小球以某一速度通过最低点C处时,小球恰好与空心管上、下壁均无挤压且无沿切线方向的加速度,AB间的距离为L,∠ABC=∠ACB=30°,CO⊥OB,静电力常量为k.
(1)作出小球在最低点C处的受力示意图,并确定固定在B点的电荷和小球的带电性质:
(2)求固定在B点电荷的电荷量大小;
(3)试求小球运动到最高点处,空心管对小球的作用力大小和方向..
(1)由小球在C点处恰好与滑槽内、外壁均无挤压且无沿切线方向的加速度,可知小球在C点的合力方向一定沿CO且指向O点,所以A处电荷对小球吸引,B处电荷对小球排斥,因为A处电荷为正,所以小球带负电,B带负电,如图所示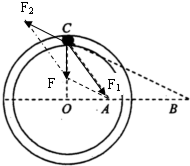 .
.
(2)因为∠ABC=∠ACB=30°,CO⊥OB,由几何关系得:BC=2ABcos30°=
L3
由于无切向加速度,小球沿切线方向的合力为零,则有:
k
cos60°=kQq L2
cos30°QBq (
L)23
解得:QB=
Q3
(3)设小球在最低点C处的速度为vC,
则:F-mg=mv 2c R
小球从C点运动到最高点的过程中,电势能不变,故由动能定理知:
2mgR=
m1 2
-v 2C
mv21 2
小球在最高点受到A、B电荷的作用力合为F,方向竖直向下
即:F+mg-F管=mv2 R
解得:F管=6mg,故空心管对小球的作用力大小为6mg,方向竖直向上.
答:(1)作出小球在最低点C处的受力示意图,并确定固定在B点的电荷和小球的带电性质:
(2)求固定在B点电荷的电荷量大小;
(3)试求小球运动到最高点处,空心管对小球的作用力大小和方向..
