问题
问答题
由相同材料的木板搭成的轨道如图,其中木板AB、BC、CD、DE、EF┅长均为L=1.5m,木板OA和其它木板与水平地面的夹角都为β=37°(sin37°=0.6,con37°=0.8),一个可看成质点的物体在木板OA上从图中的离地高度h=1.8m处由静止释放,物体与木板的动摩擦因数都为μ=0.2,在两木板交接处都用小曲面相连,使物体能顺利地经过它,既不损失动能,也不会脱离轨道.在以后的运动过程中,重力加速度取10m/s2,问: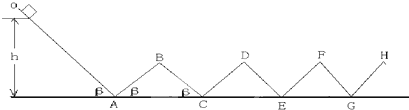
(1)物体能否静止在木板上?请说明理由.
(2)物体运动的总路程是多少?
(3)物体最终停在何处?并作出解释.
答案
(1)在斜面上物体重力沿斜面向下的分力为G1=mgsin37°=0.6mg,物体所受的摩擦力f=μmgcosθ=0.16mg.
由于f<G1,故物体在木板上停不住.
(2)从物体开始运动到最终停下的过程中,总路程为s,由动能定理得,
mgh-μmgscos37°=0-0
代入数据解得s=11.25m.
(3)假设物体依次能到达B点、D点,由动能定理得,
mg(h-Lsin37°)-μmgcos37°×(
| h |
| sin37° |
| 1 |
| 2 |
解得vB>0.
mg(h-Lsin37°)-μmgcos37°×(
| h |
| sin37° |
| 1 |
| 2 |
说明物体能通过B点,到不了D点,最终停在C点处.
答:(1)物体不能静止在木板上.
(2)物体运动的总路程为11.25m.
(3)物体最终停止在C处.
