问题
问答题
如图所示,由细管变成的竖直轨道,其圆形部分的半径为R和r,质量为m的小球从水平轨道出发,先后经过两圆形轨道最后又进入水平轨道,已知小球在A处刚好对管壁无压力,在B处对管的内侧壁压力为0.5mg,试求小球由A至B的运动过程中克服轨道阻力所做的功(细管的内径及球的大小不计).
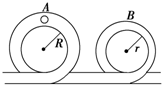
答案
在A点小球受到的重力提供向心力,
由牛顿第二定律得:mg=mv 2A R
解得:vA=
①.gR
由在B处对管的内侧壁压力为0.5mg,知mg-0.5mg=mv 2B r
解得vB=
②0.5gr
小球由A至B的运动过程中,根据动能动能定理知
mg(R-r)+W阻=
m1 2
-v 2B
m1 2
③v 2A
由①②③解得W阻=mg(
r-5 4
R)3 2
答:克服阻力做功为mg(
R-3 2
r).5 4
