半径为R的竖直放置的圆轨道与平直轨道相连，如图所示，质量为m的

问题填空题

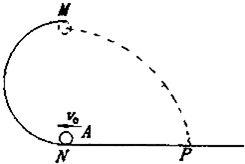
半径为R的竖直放置的圆轨道与平直轨道相连，如图所示，质量为m的小球A以一定的初速度由直轨道向左运动，并沿轨道的内壁冲上去．如果A经过N点时的速度为v₀，A经过轨道最高点M时对轨道的压力太小等于小球的重力，重力加速度为g，求：

（1）小球落地点P与N之间的距离s：

（2）取N点为零势面，小球在M点的机械能E；

（3）小球从N到M这一段过程中摩擦阻力做的功．

答案

（1）以小球为研究对象，根据牛顿第二定律得：

N+mg=m

由题：N=mg

解得：v_M=

2gR

小球离开M点后做平抛运动，则有：

竖直方向：2R=

gt2

水平方向：s=v_Mt

联立解得：s=2

（2）取N点为零势面，小球在M点的机械能为：E=E_k+E_P=

+mg•2R=3mgR

（3）小球从N到M过程，由动能定理得：

=Wf-2mgR

解得：Wf=3mgR-

答：

（1）小球落地点P与N之间的距离s为2

R：

（2）取N点为零势面，小球在M点的机械能E是3mgR；

（3）小球从N到M这一段过程中摩擦阻力做的功为3mgR-

．