问题
问答题
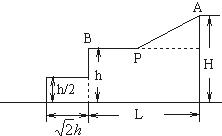
滑雪者从A点由静止沿斜面滑下,经一平台水平飞离B点,地面上紧靠着平台有一个水平台阶,空间几何尺度如图所示、斜面、平台与滑雪板之间的动摩擦因数为μ,假设滑雪者由斜面底端进入平台后立即沿水平方向运动,且速度大小不变.求:
(1)滑雪者离开B点时的速度大小;
(2)滑雪者从B点开始做平抛运动的水平距离s.
答案
(1)设滑雪者质量为m,斜面与水平面夹角为θ,滑雪者滑行过程中克服摩擦力做功
w=μmgcosθ•s+μmg(L-scosθ)=μmgL
由动能定理 mg(H-h)-μmgL=
mv2 1 2
离开B点时的速度v=2g(H-h-μL)
(2)设滑雪者离开B点后落在台阶上
=h 2
gt12,s1=vt1<1 2
h2
可解得 s1=2h(H-h-μL)
此时必须满足H-μL<2h.
当H-μL>2h时,
滑雪者直接落到地面上,h=
gt22 s2=vt21 2
可解得s2=2h(H-h-μL)
答:(1)滑雪者离开B点时的速度大小为
;2g(H-h-μL)
(2)当H-μL<2h时,滑雪者从B点开始做平抛运动的水平距离s为
.2h(H-h-μL)
当H-μL>2h时,滑雪者从B点开始做平抛运动的水平距离s为2
.h(H-h-μL)
