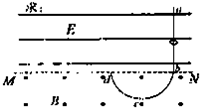
如图所示,在理想边界MN的上方有方向向右的匀强电场E,下方有垂直纸面向外的磁感应强度大小为B=0.20T的匀强磁场,电场和磁场的范围足够大.一根光滑的绝缘塑料细杆abcd弯成图示形状,其中ab段是竖直的,bcd正好构成半径为R1=0.20m的半圆,bd位于边界MN上,将一个质量为m=0.10kg、电量为q=0.50C的带正电金属环套在塑料杆ab上,从距离b点高R处由静止开始释放后,g=10m/s2.求:
(1)金属环经过最低点c处时对塑料杆的作用力;
(2)如果金属环从d点进入电场后,正好垂直打在塑料杆ab段上,求电场强度E的大小.
(1)设金属环运动到最低点C的速度为vc,
根据动能定理:mgR•2R=
m1 2 v 2c
解得:vc=
=24gR
m/s2
在最低点C处对金属环分析受力,
根据牛顿第二定律有:FN+Bqvc-mg=mv 2c R
解得:FN=5mg-Bqvc=4.72N
根据牛顿第三定律得,金属环对塑料杆的作用力为4.72N,方向向下.
(2)设金属环运动到d点时速度为vd.
根据动能定理可得:mg•R=
m1 2 v 2d
进入电场中运动,在竖直方向上只受重力作用,做竖直上抛运动,当垂直打在ab杆上时,速度的竖直分量减为零,
设时间为t1,则有0=vd-gt1
水平方向上的加速度设 为a1.
则有qE=ma1
2R=
a11 2 t 21
解得a1=20m/s2
E=4N/C
答:(1)金属环经过最低点c处时对塑料杆的作用力为4.72N,方向向下;
(2)如果金属环从d点进入电场后,正好垂直打在塑料杆ab段上,则电场强度E的大小为4N/C.
