如图1所示,斜面AB与半径为0.5m的光滑竖直圆轨道BCD相切于B点,CD部分是半圆轨道,C、D为圆轨道的最低点和最高点.将质量为0.lkg的小物块(可视为质点)从轨道的ABC部分某处由静止释放,释放点与C点的高度差为h,用力传感器测出物块经C点时对轨道的压力F,得到F与h的关系图象如图2所示.已知物块与斜面间的动摩擦因数为0.3,重力加速度g取l0m/s2.求: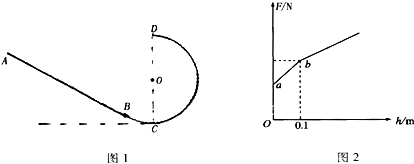
(l)图2中a、b两点的纵坐标Fa、Fb数值.
(2)物块在斜面上的释放点与B点的距离l为多大时,物块离开D点后落到轨道上与圆心O等高的位置上.
(1)图2中,h=0时,F的读数为滑块的重力,为1N;
在B点释放时,根据动能定理,有:
mgh=
m1 2
①v 2C
在C点,支持力和重力的合力提供向心力,故:
F-mg=m
②v 2C R
由①②解得:
F=mg+
h=1+2mg R
×0.1=1.4N2×1 0.5
(2)设斜面倾角为θ,由几何关系
hB=R(1-cosθ)
解得:cosθ=0.8
故sinθ=0.6
物体离开D点后,做平抛运动,有: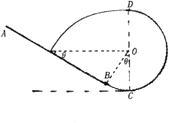
R=
gt21 2
=vDtR sinθ
物体从斜面释放到D点,由动能定理:
mglsinθ+mgR(1-cosθ)-μmglcosθ-mg•2R=
m1 2 v 2D
代入数据,得:l=3.46m
答:(l)图2中a点的纵坐标为1N,b点的纵坐标为1.4N;
(2)物块在斜面上的释放点与B点的距离l为3.46m时,物块离开D点后落到轨道上与圆心O等高的位置上.
