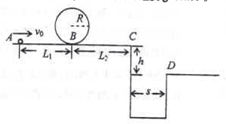
如图所示,一小滑块(体积很小,可视为质点)从A点以某一水平向右的初速度出发,沿水平直线轨道运动到B点后,进入半径R=10cm的光滑竖直圆形轨道,圆形轨道间不相互重叠,即小滑块离开圆形轨道后可继续向C点运动,C点右侧有一壕沟,C、D两点的竖直高度h=0.8m,水平距离s=1.6m,水平轨道AB长为L1=2m,BC长为L2=4m,小滑块与水平轨道间的动摩擦因数μ=0.3,重力加速度g=10m/s2.
(1)若小滑块恰能通过圆形轨道的最高点,求小滑块在A点的初速度?
(2)若小滑块既能通过圆形轨道的最高点,又不掉进壕沟,求小滑块在A点的初速度的范围是多少?
(1)小球恰能通过最高点,重力提供向心力,有:
mg=m
,v2 R
由A到最高点,由动能定理的2:
μmgL1-mg•2R=
mv2-1 2
mvA21 2
联立并代入数据解得在A点的初速度为:vA=
m/s.17
(2)若小球刚好停在C处,则有:-μmg(L1+L2)=0-
mvA′2,1 2
代入数据解得在A点的初速度为:vA′=6m/s,
若小球停在BC段,则有:
m/s≤vA≤6m/s.17
若小球能通过C点,并越过壕沟,则有h=
gt2,1 2
s=vCt
-μmg(L1+L2)=
mvC2-1 2
mvA21 2
则有:vA=2
m/s.13
初速度范围是:
m/s≤vA≤6m/s停在BC段和vA≥217
m/s越过壕沟.13
答:(1)小滑块在A点的初速度为
m/s.17
(2)小滑块在A点的初速度的范围是:
m/s≤vA≤6m/s停在BC段和vA≥217
m/s越过壕沟.13
