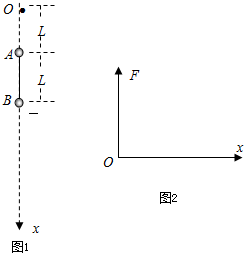
空间有一静电场,在x轴上的电场方向竖直向下,轴上的电场强度大小按E=kx分布(x是轴上某点到O点的距离),如图1所示.在O点正下方有一长为L的绝缘细线连接A、B两个均带负电的小球(可视为质点),A球距O点的距离为L,两球恰好静止,细绳处于张紧状态.已知A、B两球质量均为m,B所带电量为-q,k=
,不计两小球之间的静电力作用.mg 3qL
(1)求A球的带电量;
(2)画出A球所受电场力F与x的图象;剪断细线后,A球向上运动,求A球运动的最大速度vm;(提示:借助图2F-x图象可以确定电场力做功的规律)
(3)剪断细线后,求B球的运动范围.
(1)A、B两球静止时,A球所处位置场强为:E1=k•L=mg 3q
B球所处位置场强为:E2=k•2L=2mg 3q
对A、B由整体法得:2mg=qAE1+qE2
解得:qA=4q
(2)A球所受电场力F与x的图象如图所示:
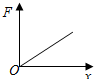
剪断细线后,A球向上运动,当A球的加速度为零时,速度达到最大,此时A球距O点距离为:
x1mg=4qE=4q
x1mg 3qL
解得:x1=3L 4
剪断细线后,A球从运动到获得最大速度,A球上升的高度为:△x1=L 4
由动能定理得:-mg△x1+
A△x1=. F
mvm2-01 2
由图象可知,可得:
A=. F
=mg+
mg4 3 2
mg7 6
解得:vm=gL 12
(本题也可由F-x图象中图线与x轴所夹的面积求电场力做功)
(3)方法一:剪断细线后,设B球向下运动的最大位移为△x时,速度变为零此时B球所受电场力为:FB=q
(2L+△x)=mg 3qL
(2L+△x)mg 3L
由动能定理得:mg△x-
B△x=0-0. F
B=. F
+2mg 3 (2L+△x)mg 3L 2
解得:△x=2L则B球的运动范围是:2L≤x≤4L
方法二:B球下落速度达到最大时,B球距O点距离为:x0mg=qE=q
x0mg 3qL
解得:x0=3L
记x0=3L位置处为O1点,小球继续下落△x位移时,其所受合力为F
F=mg-qE=mg-q
(3L+△x)=-mg 3qL
△xmg 3L
由此可以判断:B球在回复力作用下做简谐运动.
简谐运动以O1为平衡位置,振幅为L.
则B球的运动范围是:2L≤x≤4L
答:(1)A球的带电量为4q;
(2)画出A球所受电场力F与x的图象如图;剪断细线后,A球向上运动,A球运动的最大速度vm=
;gL 12
(3)剪断细线后,B球的运动范围是:2L≤x≤4L.
