问题
问答题
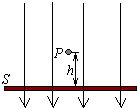
如图所示,有一质量为m,带电荷量为+q的小球(可视为质点),自竖直向下、场强为E的匀强电场中的P点静止下落.在P点正下方距离h处有一弹性绝缘挡板S(挡板不影响匀强电场的分布),小球每次与挡板S相碰后电荷量均减少到碰前的k倍(k<1),而碰撞过程中小球的机械能不损失.
(1)设匀强电场中,挡板S处电势φS=0,则电场中P点的电势φP为多少?下落前小球在P点时的电势能EP为多少?
(2)小球从P点出发后到第一次速度变为零的过程中电场力对小球做了多少功?
(3)求在以后的运动过程中,小球距离挡板的最大距离l.
答案
(1)SP之间的电压为:U=Eh
因为φS=0,
φP=Eh
所以小球在P点时的电势能EP=qEh
(2)设第一次与档板碰撞后能达到的高度为h1,由能量守恒得:
mgh+qEh=(mg+kqE)h1,
从P点出发第一次到达最高点过程中电场力对小球做的功为:
W=qEh-kqEh1
解得:W=mgqEh(1-k) mg+kqE
(3)小球与挡板碰撞后小球所带电量逐渐减小,最终电量将减小为零,整个过程中能量始终守恒,由能量守恒得:
mgh+qEh=mgl
解得:l=
hmg+qE mg
答:(1)设匀强电场中,挡板S处电势φS=0,则电场中P点的电势φP为Eh,下落前小球在P点时的电势能EP为qEh;
(2)小球从P点出发后到第一次速度变为零的过程中电场力对小球做的功为
;mgqEh(1-k) mg+kqE
(3)求在以后的运动过程中,小球距离挡板的最大距离l为
h.mg+qE mg
