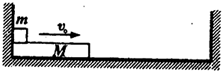
光滑的水平面上固定有左、右两竖直挡板,挡板间距离足够长,有一质量为M,长为L的长木板靠在左侧挡板处,另有一质量为m的小物块(可视为质点),放置在长木板的左端,已知小物块与长木板间的动摩擦因数为μ,且M>m,现使小物块和长木板以共同速度v0向右运动,设长木板与左一右挡板的碰撞中无机械能损失.重力加速度为g.
(1)将要发生第二次碰撞时,小物块与木板的共同速度多大?
(2)为使小物块最终不从长木板上落下,板长L应满足什么条件?
(3)若满足(2)中条件,且M=2kg,m=1kg,v0=10m/s,μ=0.6.计算整个系统在刚要发生第四次碰撞前损失的机械能和此时物块距离木板最左端的长度.
(1)选M运动方向为正方向
Mv0-mv0=(M+m)v1
v1=
v0M-m m+M
(2)由运动过程分析可知,木板第一次撞墙后,小物块相对木板向左滑行的距离最大,若此时的相对位移为s1,则
μmgs1=
(M+m)1 2
-v 20
(m+M)1 2 v 21
L≥s1时,即L≥2M (M+m)μg v 20
(3)二次撞前:Mv0-mv0=(m+M)v1
三次撞前:Mv1-mv1=(M+m)v2
四次撞前:Mv2-mv2=(M+m)v3
△E=
(m+M)1 2
-v 20
(m+M)1 2
≈149.79Jv 23
二次撞前:相对于小车向左运动s1=2M (M+m)μg v 20
三次撞前:相对于小车向右运动s2=2M (M+m)μg v 21
四次撞前:相对于小车向左运动s3=2M (M+m)μg v 22
由于物块相对于小车往复运动,故四次撞前距离小车最左端长度
d=s1-s2+s3
代入数据得d≈20m
答:(1)将要发生第二次碰撞时,小物块与木板的共同速度
v0;M-m M+m
(2)为使小物块最终不从长木板上落下,板长L应满足即L≥2M (M+m)μg
;v 20
(3)若满足(2)中条件,且M=2kg,m=1kg,v0=10m/s,μ=0.6.计算整个系统在刚要发生第四次碰撞前损失的机械能149.79J;此时物块距离木板最左端的长度约为20m.
