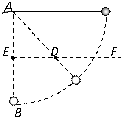
如图所示,质量为m的小球,由长为l的细线系住,线能承受的最大拉力是9mg,细线的另一端固定在A点,AB是过A的竖直线,E为AB上的一点,且AE=0.5l,过E作水平线EF,在EF上钉铁钉D,现将小球拉直水平,然后由静止释放,小球在运动过程中,不计细线与钉子碰撞时的能量损失,不考虑小球与细线间的碰撞.
(1)若钉铁钉位置在E点,求细线与钉子碰撞前后瞬间,细线的拉力分别是多少?
(2)若小球能绕钉子在竖直面内做完整的圆周运动,求钉子位置在水平线EF上距E点距离的取值.
(1)小球释放后沿圆周运动,运动过程中机械能守恒,设运动到最低点速度为v,由机械能守恒定律得:
mgl=
mv2,碰钉子瞬间前后小球运动的速率不变,碰钉子前瞬间圆周运动半径为l,碰钉子前瞬间线的拉力为F1,碰钉子后瞬间圆周运动半径为1 2
l,碰钉子后瞬间线的拉力为F2,由圆周运动、牛顿第二定律得:1 2
F1-mg=
,mv2 l
F2-mg=mv2
l1 2
得F1=3mg,F2=5mg
(2)设在D点绳刚好承受最大拉力,记DE=x1,则:AD=x12+(
)2l 2
悬线碰到钉子后,绕钉做圆周运动的半径为:r1=l-AD=l-x12+(
)2l 2
当小球落到D点正下方时,绳受到的最大拉力为F,此时小球的速度v1,由牛顿第二定律有:
F-mg=m
结合F≤9mgv12 r1
由机械能守恒定律得:mg(
+r1)=l 2
mv121 2
由上式联立解得:x1≤
l2 3
随着x的减小,即钉子左移,绕钉子做圆周运动的半径越来越大.转至最高点的临界速度也越来越大,但根据机械能守恒定律,半径r越大,转至最高点的瞬时速度越小,当这个瞬时速度小于临界速度时,小球就不能到达圆的最高点了.
设钉子在G点小球刚能绕钉做圆周运动到达圆的最高点,设EG=x2,
则:AG=
,r2=l-AG=l-x22+(
)2l 2 x22+(
)2l 2
在最高点:mg≤
由机械能守恒定律得:mg(v12 r2
-r2)=l 2
mv12联立得:x2≥1 2
l7 6
钉子位置在水平线EF上距E点距离的取值范围是:
l≤x≤7 6
l2 3
答:(1)若钉铁钉位置在E点,细线与钉子碰撞前后瞬间,细线的拉力分别是3mg和5mg;
(2)若小球能绕钉子在竖直面内做完整的圆周运动,则钉子位置在水平线EF上距E点距离的取值范围为
l≤x≤7 6
l.2 3
