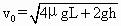问题
问答题
如图所示,同一竖直平面内固定着两水平绝缘细杆,AB=CD=L,两杆间竖直距离为h,BD两端与光滑绝缘的半圆形细杆相连,半圆形细杆与AB、CD在同一平面内,且AB、CD恰好为半圆弧在B、D两点处的切线,O为AD、CB连线的交点,在O点固定一电量为Q的正点电荷,质量为m的带负电小球P,电量为q,穿在细杆上.从A以一定初速度出发,沿杆滑动最后可以到达C点,已知小球与两水平杆间的动摩擦因数均为μ,小球所受库仑力始终小于重力.求:从A点出发时初速度的最小值.
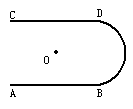
答案
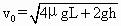

如图所示,同一竖直线上两点带电小球所受库仑力大小相等设为F,则小球在这两点所受摩擦力大小分别为
f=μ(mg-Fcosθ)
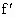 =μ(mg+Fcos)
=μ(mg+Fcos)
两处摩擦力之和为
f+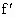 =2μmg
=2μmg
对小球从A到C过程中,由动能定理:
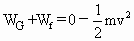
即
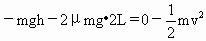
解得