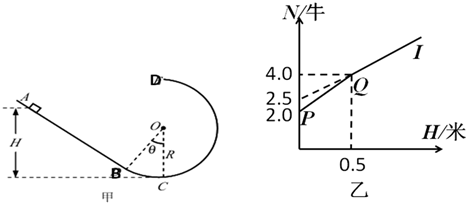
一竖直面内的轨道是由粗糙斜面AB和光滑圆轨道BCD组成,AB与BCD相切于B点,C为圆轨道的最低点.将物块置于轨道ABC上离地面高为H处由静止下滑,可用力传感器测出其经过C点时对轨道的压力N.现将物块放在ABC上不同高度处,让H从0开始逐渐增大,传感器测得物块每次从不同高度处下滑到C点时对轨道压力N,得到如图乙两段直线PQ和QI,且IQ反向延长交纵轴点坐标值为2.5N,重力加速度g取10m/s2,求:(1)小物块的质量m及圆轨道的半R=?
(2)轨道DC所对圆心角
(3)小物块与斜面AB间的动摩擦因数.
(1)从圆轨道BC下来,由动能定理可知
mgH=
mvc21 2
在C点合力提供向心力
N-mg=mvc2 R
N=
H+mg2mg R
结合PQ段图象由
mg=2N
m=0.2Kg
=2mg R 4-2 0.5
∴R=1m
(2)轨道BC所对圆心角由几何关系可知:
cosθ=
=1-0.5 1 1 2
θ=600
(3)从A到C,由动能定理可得
mgH-
=μmgcosθ(H-0.5) sinθ
mv21 2
到达C点处由向心力公式可得
N-mg= mv2 R
故:N=
(1-2mg R
)H+(mg+μ tan60°
)μ 2tan60°
k=
(1-μctg600)=2mg R 4-2.5 0.5
μ=3 4
答:(1)小物块的质量为0.2Kg及圆轨道的半径为1m
(2)轨道DC所对圆心角为60°
(3)小物块与斜面AB间的动摩擦因数3 4
