问题
问答题
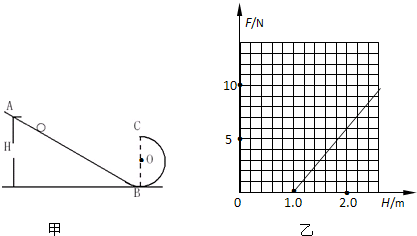
在半径为R=12000km的某星球表面,宇航员做了如下实验,实验装置如图.竖直面内的光滑轨道有轨道AB和圆轨道BC组成,将质量为m=0.1kg的小球,从轨道AB上高H处的某点静止滑下,用力传感器测出小球经过C点是对轨道的压力F,改变H的大小,可测出相应的F大小,F随H的变化关系如图乙,求:
(1)圆轨道的半径;
(2)该星球表面的重力加速度大小;
(3)该星球的第一宇宙速度.
答案
(1)小球过C点时,由牛顿第二定律得:
F+mg=m
,v 2C r2
由动能定理有:
mg(H-2r)=
mvC2-0,1 2
联立解得:F=
H-5mg,2mg r
由图可知:H1=1m时,F1=0,
即:0=
×0.5-5mg,2mg r
解得轨道半径为:r=0.4m;
(2)由图象得:H2=2m时,F2=6N,
即:6=
×2-5×0.1×g,2×0.1×g 0.4
解得:g=12m/s2;
(3)由牛顿第二定律得:
m
=mg,v2 R
第一宇宙速度为:v=
=gR 5×1.2×107
=1.2×104m/s;12×1.2×107
答:(1)圆轨道的半径为0.4m;
(2)该星球表面的重力加速度大小为12m/s2;
(3)该星球的第一宇宙速度为1.2×104m/s.
