问题
问答题
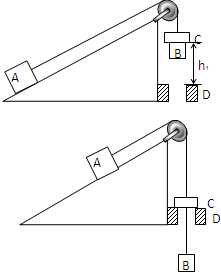
物体A放在光滑倾角37°的斜面上,与半径为r的圆柱体B用跨过定滑轮的细线相连接,半径为R的圆柱体C穿过细绳后搁在B上,三个物体的质量分别为mA=2kg,mB=mC=1kg.现让它们由静止开始运动,B下降h1=0.5m后,C被内有圆孔(半径为R′)的支架D挡住(r<R′<R),而B穿过圆孔继续下降,(滑轮的摩擦、细线和C之间的摩擦以及空气阻力均不计,且斜面足够长.g取10m/s2.)试求:
(1)圆柱体BC到达支架D时的速度;
(2)物体A在斜面上上滑的最大高度?
答案
(1)对系统运用动能定理得,(mB+mC)gh1-mAgh1sinθ=
(mA+mB+mC)v21 2
代入数据得,(1+1)×10×0.5-2×10×0.5×0.6=
×(2+1+1)v21 2
解得v=
m/s.2
(2)对A、B系统运用动能定理得,mBgh2-mAgh2sinθ=0-
(mA+mB)v2v21 2
代入数据得,1×10×h2-2×10×h2×0.6=0-
×(2+1)×(1 2
)22
解得h2=1.5m
上滑的最大高度h=(h1+h2)sinθ
解得h=1.2m.
答:(1)圆柱体BC到达支架D时的速度为
m/s;(2)物体A在斜面上上滑的最大高度为1.2m.2
