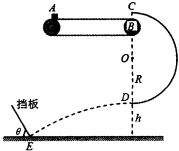
如图所示,质量为m=lkg的小物块由静止轻轻放在水平匀速运动的传送带上,从A点随传送带运动到水平部分的最右端B点,经半圆轨道C点沿圆弧切线进入竖直光滑的半圆轨道,恰能做圆周运动.C点在B点的正上方,D点为轨道的最低点.小物块离开D点后,做平抛运动,恰好垂直于倾斜挡板打在挡板跟水平面相交的E点.已知半圆轨道的半径R=0.9m,D点距水平面的高度h=0.75m,取g=10m/s2,试求:
(1)摩擦力对物块做的功;
(2)小物块经过D点时对轨道压力的大小;
(3)倾斜挡板与水平面间的夹角θ.
(1)设小物块经过C点时的速度大小
,因为经过C时恰好能完成圆周运动,由牛顿第二定律可得:v 1
mg=
,解得mv 21 R
=3m/sv 1
小物块由A到B过程中,设摩擦力对小物块做的功为W,由动能定理得:
W=1 2
,解得W=4.5Jmv 21
故摩擦力对物块做的功为4.5J.
(2)设小物块经过D点时的速度为
,对由C点到D点的过程,由动能定理的:v 2
mg.2R=1 2
-mv 22 1 2 mv 21
小物块经过D点时,设轨道对它的支持力大小为
,由牛顿第二定律得:F N
-mg=F N mv 22 R
联立解得
=60N,F N
=3v 2
m/s5
由牛顿第三定律可知,小物块对轨道的压力大小为:
=F ′N
=60N.F N
故小物块经过D点时对轨道的压力大小为60N.
(3)小物块离开D点做平抛运动,设经时间t打在E点,由h=1 2
得:t=gt 2
s15 10
设小物块打在E点时速度的水平、竖直分量分别为
、v x
,速度跟竖直方向的夹角为α,则:v y
v x =v 2
=gtv y
又tanα=
=v x v y 3
联立解得α=60°
再由几何关系可得θ=α=60°
故倾斜挡板与水平面的夹角为θ为60°.
