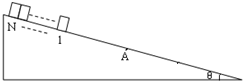
如图所示,倾角为θ的斜面A点以上部分是光滑的,A点以下部分是粗糙的,动摩擦因数为μ=2tanθ.有N个相同的小木块沿斜面靠在一起(没有粘接),总长为L,而每一个小木块可以视为质点,质量均为m.现将它们由静止释放,释放时下端与A点距离为2L,求:
(1)第1个木块通过A点时的速度;
(2)第N个木块通过A点时的速度;
(3)从第1个木块到第N个木块通过A点时的最大速度.
(1)对N个木块由动能定理得
Nmg•2Lsinθ=
Nm1 2
-0,v 21
解得v1=2
;gLsinθ
(2)木块过A点的位移为x时,摩擦力为f=μ
xmgcosθ,N L
故摩擦力正比于位移,可由平均力求摩擦力做功.
全部木块刚过A点时速度为v,则
Nmgsinθ•3L-
μNmgcosθ•L=1 2
Nmv2-01 2
解得v=
;4Lgsinθ
(3)令有n个木块过A点速度最大,则μnmgcosθ=Nmgsinθ
解得n=
,即一半木块过A点速度最大,N 2
又
Nmv2=Nmg•1 2
Lsinθ-5 2
×1 2
μNmgcosθ×1 2
L1 2
可解vm=4.5Lgsinθ
答:(1)第1个木块通过A点时的速度为2
;gLsinθ
(2)第N个木块通过A点时的速度为
;4Lgsinθ
(3)从第1个木块到第N个木块通过A点时的最大速度为4.5Lgsinθ
