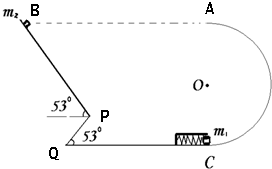
如图所示,物体质量m1=0.1kg,视为质点,在C处弹簧发射器的作用下,沿光滑半圆轨道至最高点A处后在空中飞行,不计空气阻力,恰好沿PQ方向击中P点,∠PQC=53°,半圆的半径R=0.5m,A、P两点的竖直距离为0.8米,g=10m/s2,sin53°=0.8,cos53°=0.6
(1)此物体离开A点后作什么运动?在A点速度多大?A、P两点的水平距离为多大?物体在A点对轨道的压力有多大?
(2)质量m2=0.2kg的另一物体,也视为质点,放于与A点等高的光滑斜面BP上,其倾角为53°,问:当质量m1的物体刚要离开轨道A点时,静止释放质量m2的物体应该提前还是滞后多少时间,才能实现两物体同时到达P点?
(1)物体离开A点后作平抛运动.
物体经过P点时竖直分速度为:vy=
=2ghAP
m/s=4m/s2×10×0.8
设物体在A点速度大小为vA.
据题意知:物体沿PQ方向击中P点,此时速度恰好沿PQ方向,则:vy=vAtan53°,得 vA=3m/s
物体从A运动到P的时间为:t=
=2hAP g
s=0.4s2×0.8 10
所以A、P两点的水平距离为 x=vAt=1.2m.
在A点,以物体为研究对象,根据牛顿第二定律得:
N+mg=mv 2A R
则得,N=m(
-g)=0.1×(v 2A R
-10)N=0.8N;32 0.5
根据牛顿第三定律得:物体在A点对轨道的压力N′=N=0.8N,方向竖直向上.
(2)质量m2=0.2kg的物体向下的加速度为 a=gsin53°=8m/s2.
根据xBP=
at′2,xBP=1 2
=hAP sin53°
m=1m0.8 0.8
联立解得,m2物体运动到P点的时间 t′=0.5s
所以静止释放质量m2的物体应该提前0.1s才能实现两物体同时到达P点.
答:
(1)此物体离开A点后作平抛运动,在A点速度为3m/s,A、P两点的水平距离为1.2m,物体在A点对轨道的压力为0.8N.
(2)当质量m1的物体刚要离开轨道A点时,静止释放质量m2的物体应该提前0.1s才能实现两物体同时到达P点.
