问题
解答题
已知圆C的方程为x2+y2=1，直线l1过定点A（3，0），且与圆C相切。
（1）求直线l1的方程；
（2）设圆C与x轴交于P、Q两点，M是圆C上异于P、Q的任意一点，过点A且与x轴垂直的直线为l2，直线PM交直线l2于点P′，直线QM交直线l2于点Q′，求证：以P′Q′为直径的圆C′总过定点，并求出定点坐标．
答案
解：（1）∵直线l1过点A（3，0），且与圆C：x2+y2=1相切，
设直线l1的方程为y=k（x-3），即kx-y-3k=0，
则圆心O（0，0）到直线l1的距离为d=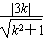
=1，解得k=±
，
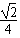∴直线l1的方程为y=±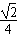
（x-3）．
（2）对于圆C：x2+y2=1，令y=0，则x=±1，即P（-1，0），Q（1，0），
又直线l2过点A且与x轴垂直，
∴直线l2的方程为x=3，
设M（s，t），则直线PM的方程为y=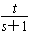
（x+1），
解方程组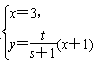
，得P′（3，
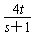），同理可得Q′（3，
），
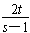∴以P′Q′为直径的圆C′的方程为（x-3）（x-3）+（y-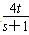
）（y-
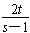）=0，
又s2+t2=1，
∴整理得（x2+y2-6x+1）+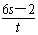
y=0，
若圆C′经过定点，只需令y=0，从而有x2-6x+1=0，解得：x=3±2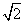
，
∴圆C′总经过定点，定点坐标为（3±2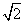，0）．