问题
选择题
过⊙O外一点P作⊙O的两条切线PA、PB,切点为A和B,若AB=8,AB的弦心距为3,则PA的长为( )
|
答案
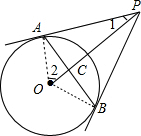
如图:连接OA,OB,
∵PA、PB为⊙O的切线,
∴OA⊥AP,OB⊥BP,PA=PB,
故PC⊥AB,且AC=BC=
AB=1 2
×8=4cm,OC=3cm,1 2
由勾股定理得OA=
=AC2+OC2
=5cm,42+32
∵∠1+∠2=90°,∠2+∠OAB=90°,
∴∠OAB=∠1,
在Rt△AOC与Rt△POA中,
∠OAB=∠1,∠2=∠2,
∴Rt△AOC∽Rt△POA,
故
=PA AC
,即PA=OA OC
=5×4 3
.20 3
故选B.
