问题
问答题
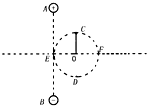
如图所示,将两个等量异种点电荷+Q和-Q分别固定于竖直线上的A、B两点,AB间距离为2d.EF为AB的中垂线.将质量为m、电荷量为+q(可视为质点且不影响原电场的分布)的带电小球固定在可绕O点自由转动的绝缘细杆的一端.从小球位于最高点C处由静止释放,已知OC=
小球经过F点时速度为v,重力加速度为g,不计细杆重力和摩擦阻力,求:d 2
(1)C、F间的电势差UCF.
(2)小球经过最低点D点的速度大小.
答案
(1)等量异种电荷形成电场是中垂线两侧电场对称,中垂线上各点的场强与中垂线垂直,且中垂线是等势线,由C到F为研究过程,由动能定理得:
mgd+qUCF=1 2
mv21 2
解之得:UCF=
…①mv2-mgd 2q
(2)据等量异种电荷电场的对称性知:UCF=UFD…②
设小球到D点的速度为VD,由C到D为研究过程,动能定理得:mgd+qUCD=
m1 2
…③v 2D
联立①②③解之得:VD=
v2
答:(1)C、F间的电势差为
;(2)小球经过最低点D点的速度大小为mv2-mgd 2q
v.2
