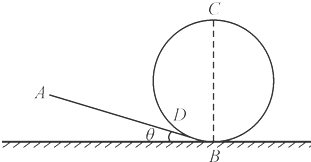
如图所示为摩托车特技比赛用的部分赛道，由一段倾斜坡道AB与竖直

问题问答题

如图所示为摩托车特技比赛用的部分赛道，由一段倾斜坡道AB与竖直圆形轨道BCD衔接而成，衔接处平滑过渡且长度不计．已知坡道的倾角θ=11.5°，圆形轨道的半径R=10m，摩托车及选手的总质量m=250kg，摩托车在坡道行驶时所受阻力为其重力的0.1倍．摩托车从坡道上的A点由静止开始向下行驶，A与圆形轨道最低点B之间的竖直距离h=5m，发动机在斜坡上产生的牵引力F=2750N，到达B点后摩托车关闭发动机．已知sin11.5°=

，g取10m/s²，求：

（1）摩托车在AB坡道上运动的加速度；

（2）摩托车运动到圆轨道最低点时对轨道的压力；

（3）若运动到C点时恰好不脱离轨道，求摩托车在BC之间克服摩擦力做的功．

答案

（1）由受力分析与牛顿第二定律可知

F+mgsinθ-kmg=ma

代入数字解得a=12m/s²

（2）设摩托车到达B点时的速度为v₁，由运动学公式可得

2ah

sinθ

，由此可得v₁=10

m/s

在B点由牛顿第二定律可知

F_N-mg=m

轨道对摩托车的支持力为F_N=1.75×10⁴N

则摩擦车对轨道的压力为1.75×10⁴N

（3）摩托车恰好不脱离轨道时，在最高点速度为v₂

由牛顿第二定律得mg=m

从B点到C点，由动能定理得-mg2R-W_f=

由此可解得W_f=1.25×10⁴J

答：（1）摩托车在AB坡道上运动的加速度为12m/s²．

（2）摩托车运动到圆轨道最低点时对轨道的压力为1.75×10⁴ N

（3）摩托车在BC之间克服摩擦力做的功为1.25×10⁴ J．