问题
问答题
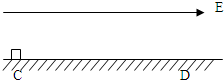
一质量为m的小滑块带正电,电荷量为q,与绝缘水平面间的动摩擦因数为μ.空间存在水平向右的匀强电场,电场强度为E.小滑块从C点由静止释放沿直线向D点运动,C、D两点间的距离为S,滑块的带电量不变,重力加速度g.
(1)求滑块运动到D点时的速度大小v;
(2)在该空间再加一垂直纸面向里的水平匀强磁场,磁感应强度为B,若滑块从C点由静止释放,运动到D点时恰好离开水平面,求离开水平面时的速度大小υ1和此过程中摩擦力对滑块所做的功W.
答案
(1)从C到D过程中,由动能定理得:
qES-μmgS=
mv2-0,1 2
解得:v=
;2(qES-μmgS) m
(2)当洛伦兹力等于滑块重力时,滑块开始离开水平面,
由平衡条件得,qBv1=mg,解得v1=
,mg qB
从C到D过程中,由动能定理得:qES+W=
mv12-0,1 2
解得:W=
-qES;m3g2 2q2B2
答:(1)求滑块运动到D点时的速度大小为
.2(qES-μmgS) m
(2)滑块离开水平面时的速度大小为
,mg qB
此过程中摩擦力对滑块所做的功
-qES.m3g2 2q2B2
