如图所示，一个质量为M的人，站在台秤上，一长为R的悬线一端系一

问题问答题

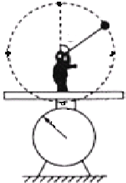
如图所示，一个质量为M的人，站在台秤上，一长为R的悬线一端系一个质量为m的小球，手拿悬线另一端，小球绕悬线另一端点在竖直平面内做圆周运动，不计空气阻力，重力加速度为g，求：

（1）若小球恰能通过圆轨道最高点，求小球通过最低点时对绳子拉力的大小．

（2）若小球恰能在竖直平面内做圆周运动，求台秤示数的最小值．

答案

（1）恰好圆周时，在最高点：mg=

mv12

从最低点到最高点，由动能定理：-2mgR=

在最低点：T-mg=m

联立以上各式解得：T=6mg

由牛顿第三定律：T′=6mg

（2）设小球经过图示位置Q点的速度为v，与竖直方向夹角为θ，则从P到Q：mgR(1-cosθ)=

在Q点：T+mgcosθ=m

得：T=3mg（1-cosθ）

其竖直方向的分量为：T_y=3mg（1-cosθ）cosθ

由数学关系可知，当cosθ=0.5，即：θ=60⁰时，T_y最小

则台秤示数的最小值为：Nmin=Mg-Ty=(M-

m)g．

答：（1）小球通过最低点时对绳子拉力的大小为6mg．

（2）台秤示数的最小值为Nmin=(M-

m)g．