质量为1.0×103kg的汽车,沿倾角为30°的斜坡由静止开始运动,汽车在运动过程中所受摩擦阻力大小恒为2000N,汽车发动机的额定输出功率为5.6×104W,开始时以a=1m/s2的加速度做匀加速运动(g=10m/s2).求:
(1)汽车做匀加速运动的时间t1;
(2)汽车所能达到的最大速率;
(3)若斜坡长143.5m,且认为汽车达到坡顶之前,已达到最大速率,则汽车从坡底到坡顶需多少时间?
(1)设汽车的牵引力为F,汽车在斜坡上受重力、支持力、摩擦力、牵引力.
根据牛顿第二定律有:F-mgsin30°-f=ma;
设匀加速的末速度为v,根据P=Fv,知道汽车的速度增加,发动机的功率也在增大,当汽车功率增加到额定输出功率时,速度继续增加,牵引力就要减小,此时匀加速运动结束.
则有:P额=Fv;
根据匀加速运动公式有:v=at1
代入数值,联立解得:匀加速的时间为:t1=7s.
(2)当达到最大速度vm时,汽车做匀速直线运动,此时F=mgsin30°+f
所以有:P额=(mgsin30°+f)vm
解得:汽车的最大速度为:vm=8m/s
(3)汽车匀加速运动的位移为:x1=
at12=24.5m1 2
在汽车达到额定功率时到汽车到达坡顶这后一阶段中,
牵引力对汽车做正功,重力和阻力做负功,设这后一阶段中时间为t2,位移为x2,根据动能定理有:
Pt2-(mgsin30°+f)x2=
mvm2-1 2
mv21 2
又有x2=x-x1
代入数值,联立求解得:t2=15s
所以汽车总的运动时间为:t=t1+t2=22s
答:(1)汽车做匀加速运动的时间是7s;
(2)汽车所能达到的最大速率是8m/s;
(3)汽车从坡底到坡顶需22s.

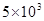 kg,在水平路面上行驶时受阻力恒定为
kg,在水平路面上行驶时受阻力恒定为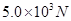 ,试求:
,试求: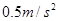 的加速度由静止开始做匀加速运动,则汽车受到的牵引力多大?
的加速度由静止开始做匀加速运动,则汽车受到的牵引力多大?