问题
问答题
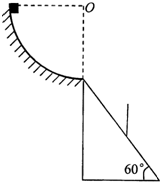
如图所示,圆心角为90°的光滑圆弧形轨道,半径为1.6m,其底端切线沿水平方向.长为
m的斜面,倾角为60°,其顶端与弧形轨道末端相接,斜面正中间有一竖直放置的直杆,现让质量为1Kg的物块从弧形轨道的顶端由静止开始滑下,物块离开弧形轨道后刚好能从直杆的顶端通过,重力加速度取10m/s2,求:16 3 5
(1)物块滑到弧形轨道底端时对轨道的压力大小;(2)直杆的长度为多大.
答案
(1)沿弧形轨道下滑过程:mgR=
mv21 2
在轨道最低点时:FN-mg=mv2 R
解得:FN=mg+
=30Nmv2 R
由牛顿第三定律可知物块对轨道的压力大小为30N
(2)根据平抛运动的规律
知x=
Lcosθ=vt ①1 2
y=
gt2 ②1 2
根据几何关系知h=
Lsinθ-y ③1 2
联立①②③式知h=2.1m
答:(1)物块滑到弧形轨道底端时对轨道的压力大小为30N;
(2)直杆的长度为2.1m.
