（1）0.33m；（2）0.67m/s；（3）1m

（1）滑块与平板车之间的最大静摩擦力f_m=μMg，设滑块与车不发生相对滑动而一起加速运动的最大加速度为a_m，以车为研究对象，则a_m== =6m/s²

以滑块和车整体为研究对象，作用在滑块上使滑块与车一起静止地加速的水平推力的最大值设为F_m，则F_m=(M+m)a_m＝36N

已知水平推力F=24N<36N，所以在F作用下M、m能相对静止地一起向右加速．

设第一次碰墙前M、m的速度为v₁，v₁==2m/s

第一次碰墙后到第二次碰前车和滑块组成的系统动量守恒

车向左运动速度减为0时，由于m<M，滑块仍在向右运动，设此时滑块的速度为v₁'，车离墙壁距离s

Mv₁－mv₁=Mv₁'

v₁'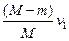＝=1m/s

以车为研究对象，根据动能定理，有－μMgs＝－mv₁²

s=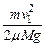=0.33m

（2）第一次碰撞后车运动到速度为零时，滑块仍有向右的速度，滑动摩擦力使车以相同的加速度重新向右加速，如果车的加速过程持续到与墙第二次相碰，则加速过程位移也为s，可算出第二次碰鲡瞬向的速度大小也为2m/s，系统的总动量将大于第一次碰墙后的动量，这显然是不可能的，可见在第二次碰墙前车已停止加速，即第二次碰墙前一些时间车和滑块已相对静止．

设车与墙壁第二次碰撞前瞬间速度为v₂，则Mv₁－mv₁=(M+m)v₂

v₂=v₁=0.67m/s

（3）车每次与墙碰撞后一段时间内，滑块都会相对车有一段向右的滑动，由于两者相互摩擦，系统的部分机械能转化为内能，车与墙多次碰撞后，最后全部机械能都转化为内能，车停在墙边，滑块相对车的总位移设为l，则有

μMgl＝(M+m)v₁²

代入数据解得l=1m