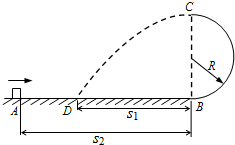
如图所示,半径R=2.5m的竖直半圆光滑轨道在B点与水平面平滑连接,一个质量m=0.50kg的小滑块(可视为质点)静止在A点.一瞬时冲量使滑块以一定的初速度从A点开始运动,经B点进入圆轨道,沿圆轨道运动到最高点C,并从C点水平飞出,落在水平面上的D点.经测量,D、B间的距离s1=10m,A、B间的距离s2=25m,滑块与水平面的动摩擦因数µ=0.20,重力加速度g=10m/s2.求:
(1)滑块刚进入圆轨道时,在B点轨道对滑块的弹力;
(2)滑块在A点受到的瞬时冲量大小.
(1)设滑块从C点飞出时的速度为vc,从C点运动到D点时间为t
滑块从C点飞出后,做平抛运动,竖直方向:2R=
gt21 2
水平方向:s1=vct
解得:vc=10m/s
设滑块通过B点时的速度为vB,根据机械能守恒定律
mvB2=1 2
mvc2+2mgR1 2
解得:vB=10
m/s2
设在B点滑块受轨道的压力为N,根据牛顿第二定律
N-mg=mv 2B R
解得:N=45N,方向竖直向上
(2)设滑块从A点开始运动时的速度为vA,根据动能定理
-μmgs2=
mvB2-1 2
mvA21 2
解得:vA=10
m/s3
设滑块在A点受到的冲量大小为I,根据动量定理
I=mvA
解得:I=5
kg•m/s;3
答:(1)滑块刚进入圆轨道时,在B点轨道对滑块的弹力大小是45N方向竖直向上;
(2)滑块在A点受到的瞬时冲量大小是5
kg•m/s.3
