问题
问答题
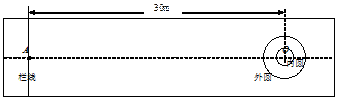
图是新兴的体育比赛“冰壶运动”的场地平面示意图。其中,内圆的半径为0.6 m,外圆的半径为1.8 m,栏线A点距内圆的圆心O点为30 m,比赛时,若参赛一方将已方的冰石壶推至内圆内,并将对方冰石壶击出外圆,则获胜。在某次比赛中,甲队队员以速度v1=3 m/s将质量为m=19 kg的冰石壶从左侧栏线A处向右推出,恰好停在O点处。乙队队员以速度v2=5 m/s将质量为M=20 kg的冰石壶也从A处向右推出,沿中心线滑动到O点并和甲队冰石壶发生碰撞。设两个冰石壶均可看成质点且碰撞前后均沿中心线运动,不计碰撞时的动能损失,两个冰石壶与水平面的动摩擦因数相同。求:
小题1:冰石壶与冰面间的动摩擦因数;
小题2: 乙队冰石壶能否停在内圆区域内并把甲队冰石壶击出外圆从而获胜。为什么?
答案
小题1:0.015
小题2:即乙获胜。
小题1:由动能定理得:-mmgs=0-mv12,m===0.015;
小题2: 乙队员抛出的冰石壶到达O’点时的速度v’:Mv22-Mv’2=mMgs,
v’==4 m/s,
两冰石壶发生弹性碰撞(设碰撞后M和m的速度分别为v’’和v3):
由Mv’=Mv’’+mv3和Mv’2=Mv’’2+mv32
解得:v3=v’=4.1 m/s,v’’==0.1 m/s,
碰撞后,甲冰石壶移动距离s1为mmgs1=mv32,s1==56 m,
乙冰石壶移动距离s2为s2==0.033 m,甲出外圆,乙在内圆,即乙获胜。
