问题
计算题
（16分）如图所示，一小球从斜轨道的某高度处自由滑下，然后沿竖直圆轨道的内侧运动。已知圆轨道的半径为R，重力加速度为g.
（1）要使小球能通过圆轨道的最高点，小球在圆轨道最高点时的速度至少为多大？
（2）如果忽略摩擦阻力，要使小球能通过圆轨道的最高点，小球的初位置必须比圆轨道最低点高出多少？
答案
（1）
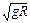
（2）h=5R/2
（1）在圆轨道的最高点，由牛顿第二定律有
mg=m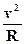
得 v=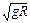
要使小球能通过圆轨道的最高点，小球在轨道最高点时的速度至少为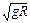
（2）设小球的初位置比圆轨道最低点高出h时，小球刚好能通过圆轨道最高点，由机械能守恒定律有mg(h-2R)=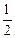 
mv2解得 h=5R/2