问题
计算题
（18分）如图所示，一个质量为m的钢性圆环套在一根固定的足够长的水平直杆上，环的半径略大于杆的半径。环与杆之间的动摩擦因数为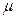
，t＝0时刻给环一个向右的初速度v0，同时对环施加一个方向始终竖直向上的力F，已知力F的大小F＝kv（k为常数，v为环的运动速度），且有kv0>mg。t＝t1时刻环开始沿杆做匀速直线运动，试求：
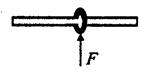
（1）t＝0时刻环的加速度；
（2）全过程中环克服摩擦力做的功；
（3）0～t1时间内环沿杆运动的距离。
答案
⑴t＝0时刻，由牛顿第二定律得 N＋mg＝F＝kυ0 （2分）
f＝μN＝ma（2分）
由以上两式解得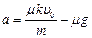 
（1分）
⑵当F＝kυ1＝mg时，环做匀速直线运动，此时速度为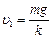
（2分）
全过程克服摩擦力做的功为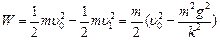
（3分）
⑶由动量定理得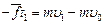 
（2分）
由于环运动过程中每一时刻有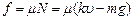 
所以有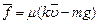 
（2分）
由以上式子得 
（2分）
环在t1时间内的位移为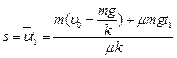 
（2分）
其他合理解答，同样给分。